สลิตเดี่ยว
สลิตเดี่ยว
การแทรกสอดของแสงผ่านสลิตเดี่ยว
ในบทเรื่อง การทดลองการแทรกสอดของยัง และ เกรตติ้งเลี้ยวเบน ผมได้อธิบายเกี่ยวกับการแทรกสอดของแสงในกรณีสลิตสองช่องและสลิตหลายช่องไปแล้วครับ แต่ในบทนี้จะอธิบายเกี่ยวกับการแทรกสอดของแสงในกรณีสลิตช่องเดียว อาจจะคิดว่าไม่มีการแทรกสอดเกิดขึ้นในกรณีของสลิตเดี่ยวนะครับ แต่ในความจริงมีการแทรกสอดครับ
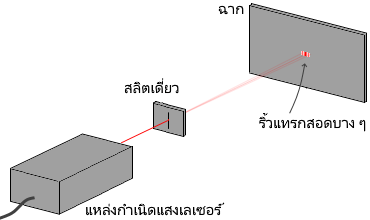 ในชุดอุปกรณ์ตามรูปด้านซ้าย เมื่อความกว้างของช่องสลิตเดี่ยวน้อยมาก ๆ จะเกิดแถบลายการแทรกสอดขึ้นบนฉากครับ หากว่ารูสลิตกว้างถึง\( \rm{ 1\;mm}\) ก็จะกว้างเกินไปแล้ว และจะปรากฏเป็นเพียงจุดบนฉากเท่านั้นครับ เมื่อบีบให้ความกว้างของสลิตมีค่าเพียงไม่กี่เท่าของความยาวคลื่นแสง \((5.0\times 10^{-7} \rm{\;m})\) แล้วแสงจะกระจายออกด้านข้างเล็กน้อย และจะเกิดแถบลายแทรกสอดขึ้นบาง ๆ ครับ
ในชุดอุปกรณ์ตามรูปด้านซ้าย เมื่อความกว้างของช่องสลิตเดี่ยวน้อยมาก ๆ จะเกิดแถบลายการแทรกสอดขึ้นบนฉากครับ หากว่ารูสลิตกว้างถึง\( \rm{ 1\;mm}\) ก็จะกว้างเกินไปแล้ว และจะปรากฏเป็นเพียงจุดบนฉากเท่านั้นครับ เมื่อบีบให้ความกว้างของสลิตมีค่าเพียงไม่กี่เท่าของความยาวคลื่นแสง \((5.0\times 10^{-7} \rm{\;m})\) แล้วแสงจะกระจายออกด้านข้างเล็กน้อย และจะเกิดแถบลายแทรกสอดขึ้นบาง ๆ ครับ
เงื่อนไขของแถบสว่าง แถบมืด
ผมจะลองหาความสัมพันธ์ของ \(d\) และ \(\lambda\) ดูนะครับโดยใช้หลักการเดี่ยวกับที่ทำในบทเรื่อง การทดลองการแทรกสอดของยัง และ เกรตติ้งเลี้ยวเบน จะมองว่าในช่องสลิตนี้มีคลื่นมูลฐาน? ที่อยู่ห่างกันเป็นระยะเท่า ๆ กัน \({12}\) แหล่งครับ
จุด \(P_1\) (กรณีที่ \(d\sin\theta_1=\lambda\))
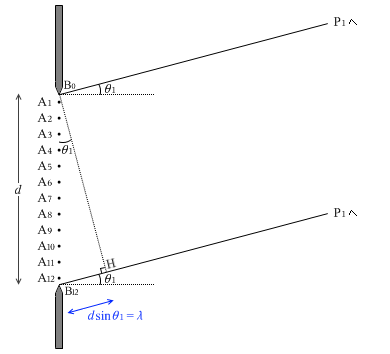 กำหนดให้ความกว้างสลิตเท่ากับ \(d\) และมองว่ามีคลื่นมูลฐานออกมาจากทุก ๆ จุด \({\rm A_1}\)ถึง \({\rm A_{12}}\) ดังในรูปด้านซ้ายนะครับ ตอนนี้จะกำหนดให้ปลายบนสลิต คือ \({\rm B_0}\) ปลายล่างสลิตคือ \({\rm B_{12}}\) ระยะห่างระหว่าง \({\rm B_0}\) ถึง \({\rm A_1}\) และ \({\rm A_{12}}\) ถึง \({\rm B_{12}}\) มีค่าเป็นครึ่งหนึ่งของระยะจาก \({\rm A_1}\) ถึง \({\rm A_2}\) จะกำหนดให้ \({\rm P_1}\) และ \(\theta_1\) เป็นจุดและมุมที่ทำให้สมการด้านล่างนี้เป็นจริงครับ
กำหนดให้ความกว้างสลิตเท่ากับ \(d\) และมองว่ามีคลื่นมูลฐานออกมาจากทุก ๆ จุด \({\rm A_1}\)ถึง \({\rm A_{12}}\) ดังในรูปด้านซ้ายนะครับ ตอนนี้จะกำหนดให้ปลายบนสลิต คือ \({\rm B_0}\) ปลายล่างสลิตคือ \({\rm B_{12}}\) ระยะห่างระหว่าง \({\rm B_0}\) ถึง \({\rm A_1}\) และ \({\rm A_{12}}\) ถึง \({\rm B_{12}}\) มีค่าเป็นครึ่งหนึ่งของระยะจาก \({\rm A_1}\) ถึง \({\rm A_2}\) จะกำหนดให้ \({\rm P_1}\) และ \(\theta_1\) เป็นจุดและมุมที่ทำให้สมการด้านล่างนี้เป็นจริงครับ
\(|{\rm B_0 P_1-B_{12} P_1}|=\lambda\)
เนื่องจาก\(|{\rm B_0 P_1-B_{12} P_1}|\) ก็คือ \(d\sin\theta_1\) ดังนั้นพูดอีกอย่างคือเรากำหนด \({\rm P_1}\) และ \(\theta_1\) เป็นจุดและมุมที่สอดคล้องกับสมการ
\(d\sin\theta_1=\lambda\)
นั่นเองครับ
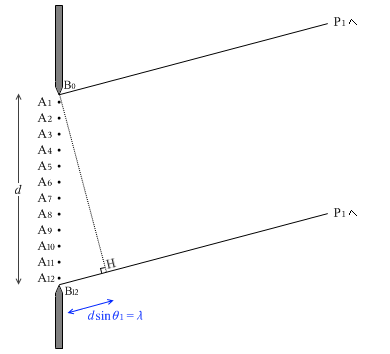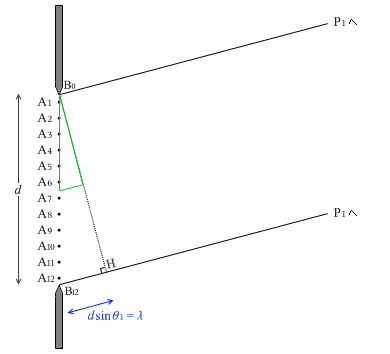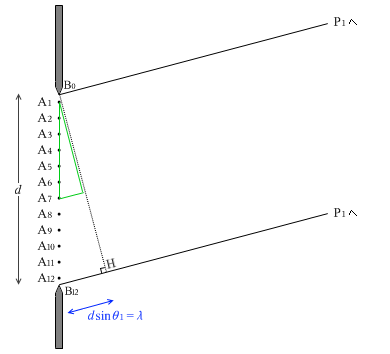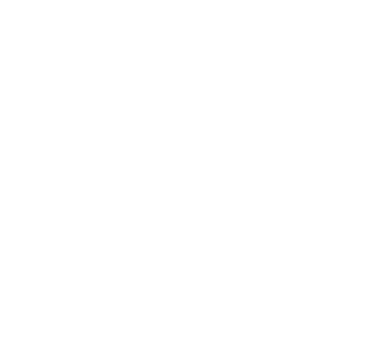 จะมีคลื่นมูลฐานเดินทางออกจากทุก ๆ จุด \({\rm A_1-A_{12}}\) และมุ่งหน้าไปยังจุด \({\rm P_1}\) นะครับ ทีนี้ลองพิจารณาดูสามเหลี่ยมคล้ายที่เล็กกว่า \(\triangle{\rm B_{12} B_0 H}\) ครึ่งหนึ่ง ฐานของสามเหลี่ยมนี้มีความยาว \({\large\frac{1}{2}}\lambda\)ครับ เมื่อเลื่อนสามเหลี่ยมนี้ลงไปด้านล่างเล็กน้อย จะไปสบกับจุดยอด \({\rm A_1}\) และ \({\rm A_7}\) พอดีครับ ดังนั้นจะเห็นว่า
จะมีคลื่นมูลฐานเดินทางออกจากทุก ๆ จุด \({\rm A_1-A_{12}}\) และมุ่งหน้าไปยังจุด \({\rm P_1}\) นะครับ ทีนี้ลองพิจารณาดูสามเหลี่ยมคล้ายที่เล็กกว่า \(\triangle{\rm B_{12} B_0 H}\) ครึ่งหนึ่ง ฐานของสามเหลี่ยมนี้มีความยาว \({\large\frac{1}{2}}\lambda\)ครับ เมื่อเลื่อนสามเหลี่ยมนี้ลงไปด้านล่างเล็กน้อย จะไปสบกับจุดยอด \({\rm A_1}\) และ \({\rm A_7}\) พอดีครับ ดังนั้นจะเห็นว่า
\(|{\rm A_1 P_1-A_7 P_1} | = {\large\frac{1}{2}}\lambda\)
ดังที่ได้อธิบายไปในบท การทดลองการแทรกสอดของยัง การที่ผลต่างเส้นทางเดินของแสง Path Difference (PD) \(|{\rm A_1 P_1-A_7 P_1} |\) เท่ากับ \({\large\frac{1}{2}}\lambda\) หมายความว่าคลื่นแสงที่เดินทางออกจากจากจุด \({\rm A_1}\) และ \({\rm A_7}\) จะหักล้างกันที่จุด \({\rm P_1}\) และมืดลงครับ
ในทำนองเดียวกัน \({\rm A_2}\) และ \({\rm A_8}\), \({\rm A_3}\) และ \({\rm A_9}\), \({\rm A_4}\) และ \({\rm A_{10}}\), \({\rm A_5}\) และ \({\rm A_{11}}\), \({\rm A_6}\) และ \({\rm A_{12}}\) จะหักล้างกันครับ ท้ายที่สุดแล้วทั้งหมดจะหักล้างกันและจุด \({\rm P_1}\) จะมืดลงครับ
นั่นคือ จุด \({\rm P_1}\) ที่ทำให้ \(d\sin\theta_1=\lambda\) จะเป็นจุดที่มืดลงครับ
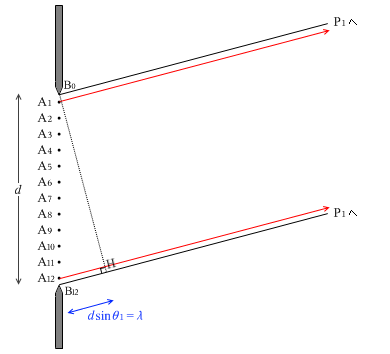 ทีนี้ เมื่อลองดู \({\rm A_1}\) เทียบกับ \({\rm A_{12}}\) แล้ว PD ประมาณ \(\lambda\) คุณอาจจะคิดสินะครับว่า ดังนั้นจะ แทรกสอดแบบเสริมกันและจุด \({\rm P_1}\) จะสว่างขึ้นมา แต่ว่าไม่เป็นเช่นนั้นครับ จริงอยู่ที่สันคลื่นของ \({\rm A_1}\) และสันคลื่นของ \({\rm A_{12}}\) จะเสริมกันที่จุด \({\rm P_1}\) และเกิดเป็นสันคลื่นใหญ่ขึ้นมา แต่ว่าในขณะเดียวกันท้องคลื่นของ \({\rm A_6}\) และท้องคลื่นของ \({\rm A_7}\) ก็จะเสริมกันที่จุด \({\rm P_1}\) และเกิดเป็นท้องคลื่นใหญ่ขึ้นมาเช่นกันครับ สุดท้ายแล้วสันคลื่นใหญ่และท้องคลื่นใหญ่ก็จะหักล้างกันครับ ในทำนองเดียวกัน \({\rm A_2}\),\({\rm A_{11}}\),\({\rm A_5}\),\({\rm A_8}\) สี่อันก็จะหักล้างกัน และ \({\rm A_3}\),\({\rm A_{10}}\),\({\rm A_4}\),\({\rm A_9}\) อีกสี่อันก็จะหักล้างกันครับ
ทีนี้ เมื่อลองดู \({\rm A_1}\) เทียบกับ \({\rm A_{12}}\) แล้ว PD ประมาณ \(\lambda\) คุณอาจจะคิดสินะครับว่า ดังนั้นจะ แทรกสอดแบบเสริมกันและจุด \({\rm P_1}\) จะสว่างขึ้นมา แต่ว่าไม่เป็นเช่นนั้นครับ จริงอยู่ที่สันคลื่นของ \({\rm A_1}\) และสันคลื่นของ \({\rm A_{12}}\) จะเสริมกันที่จุด \({\rm P_1}\) และเกิดเป็นสันคลื่นใหญ่ขึ้นมา แต่ว่าในขณะเดียวกันท้องคลื่นของ \({\rm A_6}\) และท้องคลื่นของ \({\rm A_7}\) ก็จะเสริมกันที่จุด \({\rm P_1}\) และเกิดเป็นท้องคลื่นใหญ่ขึ้นมาเช่นกันครับ สุดท้ายแล้วสันคลื่นใหญ่และท้องคลื่นใหญ่ก็จะหักล้างกันครับ ในทำนองเดียวกัน \({\rm A_2}\),\({\rm A_{11}}\),\({\rm A_5}\),\({\rm A_8}\) สี่อันก็จะหักล้างกัน และ \({\rm A_3}\),\({\rm A_{10}}\),\({\rm A_4}\),\({\rm A_9}\) อีกสี่อันก็จะหักล้างกันครับ
พูดอีกอย่าง ไม่ว่าเราจะรวมกลุ่มแบบไหนก็ตาม จุด \({\rm P_1}\) ก็จะมืดลงเมื่อ \(d\sin\theta_1=\lambda\) ครับ
จุด \(P_2\) (กรณีที่ \(d\sin\theta_2={\large\frac{3}{2}}\lambda\))
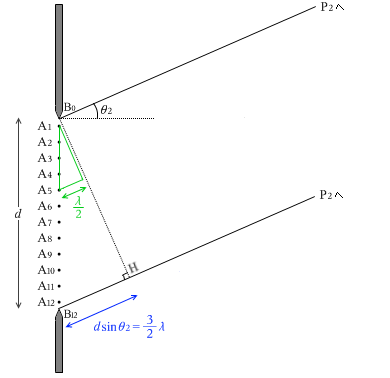 ต่อไปจะเพิ่มมุมอีกเล็กน้อยแล้วลองพิจารณากรณีที่ \(d\sin\theta_2={\large\frac{3}{2}}\lambda\) นะครับ
ต่อไปจะเพิ่มมุมอีกเล็กน้อยแล้วลองพิจารณากรณีที่ \(d\sin\theta_2={\large\frac{3}{2}}\lambda\) นะครับ
คราวนี้ จะพิจารณาสามเหลี่ยมรูปที่มีคล้ายกับ \(\triangle{\rm B_{12} B_0 H}\) และมีเล็กเป็น \({\large\frac{1}{3}}\) เท่านะครับ จะเห็นว่าสามเหลี่ยมนี้มีฐานยาว \({\frac{1}{2}}\lambda\) ครับ เมื่อเลื่อนสามเหลี่ยมนี้ลงมาด้านล่างเล็กน้อย จุดยอดจะไปสบกับจุด \({\rm A_1}\) และ \({\rm A_5}\)พอดี ครับ ดังนั้นจะได้ว่า
\(|{\rm A_1 P_2-A_5 P_2}| = {\large\frac{1}{2}}\lambda \)
ครับ กล่าวคือ คลื่นแสงที่เดินทางออกจากจากจุด \({\rm A_1}\) ที่เดินทางไปถึงจุด \({\rm P_2}\) และ คลื่นแสงที่เดินทางออกจากจากจุด \({\rm A_5}\) ที่เดินทางไปถึงจุด \({\rm P_2}\) จะหักล้างกันครับ ในทำนองเดียวกัน \({\rm A_2}\) และ \({\rm A_6}\), \({\rm A_3}\) และ \({\rm A_7}\), \({\rm A_4}\) และ \({\rm A_8}\) จะหักล้างกันครับ ดังนั้นจะคงเหลือ \({\rm A_9}\),\({\rm A_{10}}\),\({\rm A_{11}}\),\({\rm A_{12}}\) ครับ ดังนั้นจุด \({\rm P_2}\) จะเป็นจุดสว่างเพราะคลื่น \(4\) คลื่นที่เหลืออยู่นี้ครับ
ถ้าจะพูดอีกอย่าง แทนที่จะพูดว่าเหลือ \({\rm A_9}\),\({\rm A_{10}}\),\({\rm A_{11}}\),\({\rm A_{12}}\) แล้วล่ะก็ จะอารมณ์ประมาณนี้ครับ
\({\rm A_1+A_5+A_9}\) =สัน+ท้อง+สัน=สัน \({\rm A_2+A_6+A_{10}}\)=สัน+ท้อง+สัน=สัน \({\rm A_3+A_7+A_{11}}\)=สัน+ท้อง+สัน=สัน \({\rm A_4+A_8+A_{12}}\)=สัน+ท้อง+สัน=สันด้วยเหตุนี้ จุด \({\rm P_2}\) ที่สอดคล้องกับสมการ \(d\sin\theta_2={\large\frac{3}{2}}\lambda\) จะกลายเป็นจุดสว่างครับ
จุด \({\rm P_0}\) (กรณีที่ \(d\sin\theta=0\))
ในกรณีที่ \(\theta=0\) ซึ่งก็คือคลื่นที่เคลื่อนที่ไปตรง ๆ ด้านหน้าสลิต (เรียกจุดที่อยู่ด้านสลิตตรง ๆ จุดนี้ว่าจุด \({\rm P_0}\)) นั้นจะไม่มีการเลื่อน##เฟส (ยกตัวอย่างเช่น ถ้าหากคลื่นที่ออกจากจุด \({\rm A_1}\) เป็นสันคลื่น คลื่นที่ออกจากจุด \({\rm A_2 ~ A_{12} }\) ก็จะเป็นสันคลื่นด้วย) จุด \({\rm P_0}\) จะเป็นจุดสว่างครับ
กรณีที่ \(d\sin\theta={\large\frac{1}{2}}\lambda\)
ในกรณีที่ \(d\sin\theta={\large\frac{1}{2}}\lambda\) (ระหว่างจุด \({\rm P_0}\) และ \({\rm P_1}\)) นั้น แม้ว่าเมื่อคิดด้วยหลักการเดียวกันกับกรณีที่ \(d\sin\theta_2={\large\frac{3}{2}}\lambda\) จะเข้าใจว่า จุดนี้สว่างขึ้น แต่จุด \({\rm P_0}\) ของกรณีที่ \(d\sin\theta=0\) ก็จะสว่างขึ้นเช่นเดียวกัน ดังนั้นจึงไม่สามารถแยกแยะจุด \({\rm P_0}\) ออกจากกรณีนี้ได้ครับ 「สว่าง,สว่าง,มืด,สว่าง,มืด,...」เมื่อลองเรียงลำดับดูเช่นนี้แล้ว จะไม่สามารถรับรู้ถึงจุด「สว่าง」ในลำดับที่สองได้ครับ
ทำให้เป็นรูปทั่วไป
เมื่อมองว่า คลื่นมูลฐานนั้นไม่ได้มี \(12\) ลูก แต่มีจำนวนมากกว่านั้นมาก ๆ ดูแล้ว จะกลายเป็นเรื่องที่ซับซ้อนไปเลยครับ แต่ถ้าลองคิดตามแบบด้านล่างนี้ดูจะทำให้เข้าใจง่ายขึ้นครับ
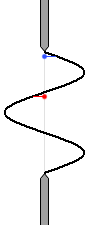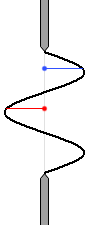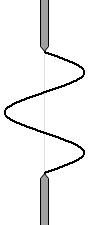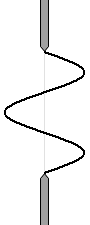 การที่คลื่นหักล้างกัน##linkนั้นก็คือคลื่นที่มีเฟสตรงข้ามกัน##linkมาปะทะกันครับ เพื่อที่จะคิดเฟสนั้น ลองวาดรูปคลื่นออกมาเลยครับ
คลื่นที่ออกมาจากจุดสีฟ้า และ คลื่นที่ออกมาจากจุดสีแดง ในรูปด้านซ้ายนี้ มีเฟสตรงข้ามกัน ดังนั้นจะหักล้างกันครับ
การที่คลื่นหักล้างกัน##linkนั้นก็คือคลื่นที่มีเฟสตรงข้ามกัน##linkมาปะทะกันครับ เพื่อที่จะคิดเฟสนั้น ลองวาดรูปคลื่นออกมาเลยครับ
คลื่นที่ออกมาจากจุดสีฟ้า และ คลื่นที่ออกมาจากจุดสีแดง ในรูปด้านซ้ายนี้ มีเฟสตรงข้ามกัน ดังนั้นจะหักล้างกันครับ
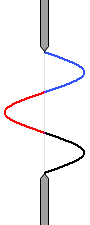 หากว่ามีบริเวณสีดำที่ไม่ได้หักล้างกันไปหลงเหลืออยู่ ฉากก็จะสว่างขึ้นครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta={\large\frac{3}{2}}\lambda\) ที่อธิบายไปด้านบนครับ
หากว่ามีบริเวณสีดำที่ไม่ได้หักล้างกันไปหลงเหลืออยู่ ฉากก็จะสว่างขึ้นครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta={\large\frac{3}{2}}\lambda\) ที่อธิบายไปด้านบนครับ
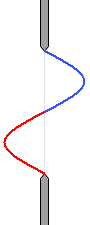 หากว่าไม่มีบริเวณสีดำหลงเหลืออยู่ ฉากก็จะมืดลงครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta=\lambda\) ที่อธิบายไปด้านบนครับ
หากว่าไม่มีบริเวณสีดำหลงเหลืออยู่ ฉากก็จะมืดลงครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta=\lambda\) ที่อธิบายไปด้านบนครับ
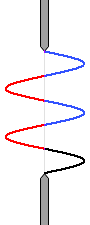 หากว่ามีบริเวณสีดำหลงเหลืออยู่เพียงเล็กน้อย ฉากก็จะสว่างขึ้นเพียงเล็กน้อยครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta={\large\frac{5}{2}}\lambda\) ครับ
หากว่ามีบริเวณสีดำหลงเหลืออยู่เพียงเล็กน้อย ฉากก็จะสว่างขึ้นเพียงเล็กน้อยครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta={\large\frac{5}{2}}\lambda\) ครับ
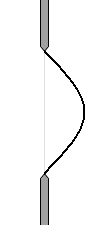 หากว่ามีบริเวณสีดำหลงเหลืออยู่มาก ฉากก็จะสว่างขึ้นมากเช่นกันครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta={\large\frac{1}{2}}\lambda\) ครับ
หากว่ามีบริเวณสีดำหลงเหลืออยู่มาก ฉากก็จะสว่างขึ้นมากเช่นกันครับ
รูปด้านซ้ายนี้ สอดคล้องกับกรณีที่ \(d\sin\theta={\large\frac{1}{2}}\lambda\) ครับ
 กรณีที่ส่องสว่างมากกว่านั้นอีกคือกรณีที่คล้ายกับในรูปด้านซ้ายครับ
แม้ว่าบริเวณสีดำจะเป็นคลื่นที่ไม่ได้หักล้างกันก็จริง แต่การเลื่อนเฟสก็ยังคงอยู่ไม่เปลี่ยนแปลง และยังมีการหักล้างเกิดขึ้นบ้างเล็กน้อยครับ การหักล้างกันของในรูปด้านซ้ายจะน้อยกว่าการหักล้างกันในรูปด้านบนครับ เพราะว่าแทบจะไม่มีความต่างเฟสเลย่
กรณีที่ส่องสว่างมากกว่านั้นอีกคือกรณีที่คล้ายกับในรูปด้านซ้ายครับ
แม้ว่าบริเวณสีดำจะเป็นคลื่นที่ไม่ได้หักล้างกันก็จริง แต่การเลื่อนเฟสก็ยังคงอยู่ไม่เปลี่ยนแปลง และยังมีการหักล้างเกิดขึ้นบ้างเล็กน้อยครับ การหักล้างกันของในรูปด้านซ้ายจะน้อยกว่าการหักล้างกันในรูปด้านบนครับ เพราะว่าแทบจะไม่มีความต่างเฟสเลย่
สอดคล้องกับกรณีที่ \(d\sin\theta\approx 0\) ครับ นี่คือแสงที่ส่องสว่างบริเวณรอบ ๆ จุด \({\rm P_0}\) ครับ
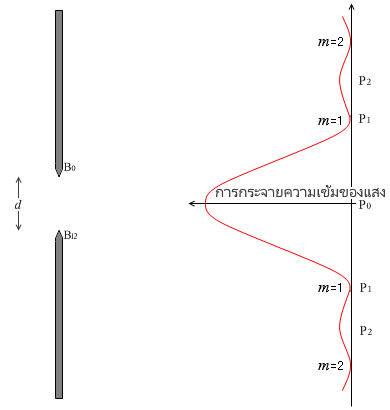 ดังนี้แล้ว เมื่อแสงสีเดียวเดินทางผ่านสลิตเดี่ยวแล้ว การกระจายความเข้มของแสงที่ตกกระทบฉากก็จะเป็นดังรูปซ้ายมือนี้ครับ
ดังนี้แล้ว เมื่อแสงสีเดียวเดินทางผ่านสลิตเดี่ยวแล้ว การกระจายความเข้มของแสงที่ตกกระทบฉากก็จะเป็นดังรูปซ้ายมือนี้ครับ
เมื่อลองสรุปเนื้อหาสลิตเดี่ยวด้านบนทั้งหมดดูจะได้ตามด้านล่างนี้ครับ โดยคร่าว ๆ แล้วจะตรงข้ามกับกรณีของเกรตติ้งเลี้ยวเบนครับ
สลิตเดี่ยว
เงื่อนไขที่ทำให้เกิดริ้วสว่าง \(\boldsymbol{{\large\frac{dx}{l}}=0 \, ,(m+{\large\frac{1}{2}})\lambda}\)
เงื่อนไขที่ทำให้เกิดริ้วมืด \(\boldsymbol{{\large\frac{dx}{l}}=m\lambda}\)
\((m=1,2,3,...)\)
\(m\) ไม่ใช่ \((m=0,1,2,...)\) แต่เป็น \((m=1,2,3,...)\) นะครับ
การแข่งขันกันของเกรตติ้งเลี้ยวเบนและสลิตเดี่ยว
ถ้าลองเปรียบเทียบสมการเงื่อนไขของสลิตเดี่ยวและของเกรตติ้งเลี้ยวเบนดู และนำสลิตเดี่ยวหลาย ๆ อันมาเรียงต่อกันเป็นเกรตติ้งเลี้ยวเบน อาจจะเกิดความสงสัยว่า จุดที่เป็นไปตามเงื่อนไข \(d\sinθ = λ\) นั้น จริง ๆ แล้วจะสว่างหรือมืด สินะครับ จริงอยู่ครับที่ \(d\) ในสมการเงื่อนไขของเกรตติ้งเลี้ยวเบนคือระยะห่างระหว่างแต่ละสลิต ในขณะที่ \(d\) ในสมการเงื่อนไขของสลิตเดี่ยวคือความกว้างของสลิต และเป็นปริมาณที่แตกต่างกันสองตัว แต่ถ้าค่า \(d\) ของทั้งคู่มีค่าเท่ากัน และ \(\sinθ\) ก็มีค่าเท่ากันด้วยแล้ว ตำแหน่งที่มุมนี้ชี้ไปนั้น ควรจะส่องสว่างขึ้นหากเป็นไปตามสมการเงื่อนไขของเกรตติ้งเลี้ยวเบน แต่ว่าหากเป็นไปตามสมการเงื่อนไขของสลิตเดี่ยวแล้วมันจะมืดลงไปครับ เช่นในกรณีที่ความกว้างสลิตมีค่าเท่ากับ \(\rm{0.1\;mm}\) และระยะห่างระหว่างสลิตก็มีค่าเท่ากับ \(\rm{0.1\;mm}\) ครับ
ในกรณีแบบนี้เนื่องจากแสงที่พุ่งออกมาจากสลิตจะมืด ดังนั้นอย่างไรก็ตาม(จุดนั้น)ก็จะมืดลงไปครับ
เพื่อจะป้องกันเรื่องแบบนี้ จะต้องทำให้ความกว้างของสลิตเล็กลงครับ เมื่อทำเช่นนั้นแล้ว ค่าของ \(\sinθ\) ก็จะเพิ่มขึ้น (นี่คือ \(\sinθ\) ในสมการเงื่อนไขของสลิตเดี่ยวครับ) ทำให้ไม่ไปชนกับค่า \(\sinθ\) ของสมการเงื่อนไขของเกรตติ้งเลี้ยวเบนอีกต่อไปครับ
ด้วยเหตุนี้จึงได้ว่า เกรตติ้งเลี้ยวเบนที่มีความกว้างของสลิตหนึ่ง ๆ น้อยกว่าระยะห่างระหว่างแต่ละสลิตจะมีคุณภาพที่ดีครับ
ความคิดเห็น
แสดงความคิดเห็น