การทดลองการแทรกสอดของแสงโดยวิธีของยัง
การทดลองการแทรกสอดของแสงโดยวิธีของยัง
ปรากฏการณ์การแทรกสอดของคลื่น##linkนั้นมีรูปแบบต่าง ๆ มากมาย
เช่นการแทรกสอดของคลื่นผิวน้ำหรือ
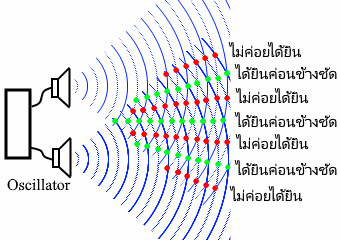หรือการแทรกสอดของคลื่นเสียง##linkเป็นต้นครับ
ในบทความนี้จะทำการอธิบายเกี่ยวกับการแทรกสอดของคลื่นแสง##link(โดยเฉพาะรังสีแสงช่วงที่มองเห็นได้)ที่มาจากแหล่งกำเนิดสองจุดครับ
เมื่อคลื่นแสงลูกหนึ่งกับคลื่นแสงอีกลูกหนึ่งปะทะกันแล้ว จะแทรกสอดแบบเสริมกันหรือหักล้างกันนั้น สามารถตรวจสอบด้วยฉากได้ครับ จุดที่แทรกสอดแบบเสริมกันจะสว่างขึ้น จุดที่แทรกสอดแบบหักล้างกันจะมืดลงครับ บนฉากรับนั้นจุดมืดและจุดสว่างเหล่านี้จะปรากฏสลับไปสลับมา ทำให้เกิดเป็นริ้วขึ้นได้ เรียกว่าริ้วการแทรกสอดครับ
การทดลองการแทรกสอดของแสงโดยวิธีของยัง
การวางแผนเตรียมการของยัง
แม้ว่าในการแทรกสอดของคลื่นผิวน้ำหรือคลื่นเสียง การสร้างคลื่นที่มีความยาวคลื่นเท่ากันและเฟส##linkตรงกันจากแหล่งกำเนิดสองแหล่งจะเป็นเรื่องที่ง่าย แต่สำหรับคลื่นแสงแล้ว นี่ไม่ใช่เรื่องง่ายเลยครับ
ความยาวของคลื่นแสง (ในช่วงที่ตามองเห็น) นั้นเป็นสิ่งที่เล็กมากๆ แต่เมื่อเปรียบเทียบกันแล้ว หลอดไฟที่เป็นแหล่งกำเนิดคลื่นแสงนั้นมีขนาดใหญ่กว่าความยาวคลื่นแสงมากเกินไปครับ แสงเปล่งออกมาจากจุดใด และ แสงที่ออกมานั้นเป็นอย่างไรเป็นสิ่งที่ไม่สามารถระบุได้ครับ
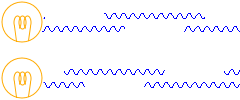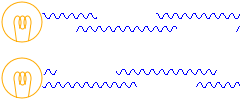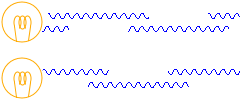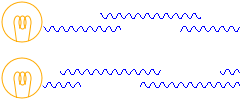นอกจากนี้ หลอดไฟนั้น ไม่สามารถทำการปล่อยคลื่นแสงออกมาอย่างต่อเนื่องสม่ำเสมอได้ครับ ไม่ว่าอย่างไรก็ตามคลื่นจะถูกตัดขาดกลางทางไปครับ เพราะเหตุนี้ เฟสของคลื่นที่ออกมาจากหลอดไฟสองดวงจะเหลื่อมกันมากน้อยแค่ไหน จึงไม่สามารถระบุได้ครับ
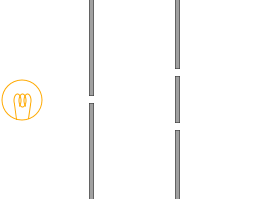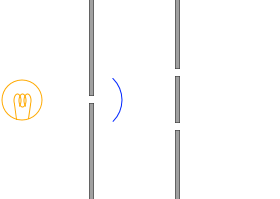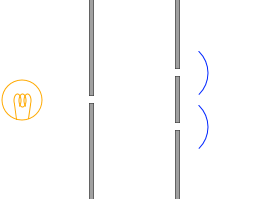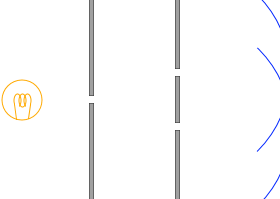เพื่อแก้ไขปัญหาเหล่านี้ยัง
นักฟิสิกส์ชาวอังกฤษในศตวรรษที่ 19 โทมัส ยัง (Thomas Young)
ได้วางแผนทำการวางแผนตามรูปซ้ายครับ สลิตเดี่ยว
"สลิต" (Slit) คือร่องที่เล็กมาก ๆ ครับ ในการทดลอง เราจะนำกระจกสไลด์มาเคลือบด้วยน้ำหมึกดำ แล้วขูดให้เป็นรอยด้วยใบมีดโกนเพื่อสร้างร่องขึ้นครับ
ในด่านแรกจะบีบให้เหลือคลื่นเพียงหนึ่งคลื่น
นึกภาพของคลื่นมูลฐานหนึ่งคลื่น##linkครับ แน่นอนว่าไม่ใช่สิ่งที่สามารถนับแบบเป๊ะ ๆ ว่า 「\(1\) คลื่น」「\(2\) คลื่น」ได้ครับ
และปล่อยให้คลื่นนี้ผ่านไปยังสลิตสองอันซึ่งอยู่ห่างจากสลิตเดี่ยวนี้เป็นระยะทางเท่ากัน เมื่อทำเช่นนี้แล้ว คลื่นสองชุดที่มีเฟสตรงกันก็จะถูกปล่อยออกมาจากสลิตคู่ในขั้นที่สองได้อย่างแท้จริงครับ
สำหรับคำถามที่ว่า "ทำไมจะต้องดำเนินการสองขั้นตอนแบบนี้" ผมไม่สามารถอธิบายละเอียดกว่านี้ได้แล้วครับ สำหรับคนที่อยากจะเข้าใจอย่างลึกซึ้งมากกว่านี้ ลองค้นด้วยคำว่า 「คุณสมบัติโคฮีเรนต์ของแสง Coherence, Optics」 ดูนะครับ
เรียกการเตรียมสลิตในลักษณะนี้เพื่อทำการทดลองสังเกตปรากฏการณ์แทรกสอดของแสงว่าการทดลองการแทรกสอดของแสงโดยวิธีของยัง การทดลองนี้ได้แสดงให้เห็นการแทรกสอดของแสงและได้พิสูจน์ว่าแสงเป็นคลื่นครับ
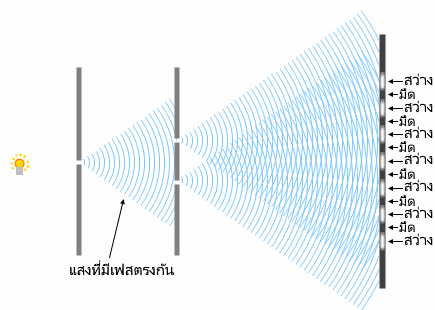(อาจจะโต้แย้งสินะครับ แต่ว่ารูปซ้ายมือนี้เป็นรูปที่วาดขึ้นในสเกลที่ใหญ่เกินจริงไปมากเพื่อให้เข้าใจได้ง่ายครับ ในความเป็นจริงแล้ว ไม่เพียงแต่แสงจะไม่กระจายออกกว้างขนาดนี้แล้ว ความกว้างของสลิตก็จะน้อยกว่า \(\rm{1\;mm}\) ด้วย และระยะจากสลิตคู่ไปถึงฉากก็จะมากกว่า \(\rm{1\;m}\) ด้วยครับ)
(นอกจากนี้ แม้ว่าในรูปซ้ายมือผมได้ทำการวาดภาพประกอบรูปคล้าย ๆ หลอดไส้แทนแหล่งกำเนิดแสง แต่ความเป็นจริงแล้ว เวลาทำการทดลอง จะดีมากครับถ้าใช้แสงคลื่นความถี่เดียว (แสงสีเดียวเช่น แสงเลเซอร์) ส่วนหลอดไส้นั้นจะทำให้คลื่นในช่วงความยาวคลื่นต่าง ๆ ถูกปล่อยออกมา ดังนั้นริ้วการแทรกสอดจะเบลอไปได้ครับ)
(หากว่าใช้แสงเลเซอร์เป็นแหล่งกำเนิดแสง สลิตเดี่ยวในขั้นตอนแรกก็จะไม่จำเป็นครับ แต่ ไม่สามารถใช้แสงเลเซอร์สองอันแทนแหล่งกำเนิดแสงสองแหล่งแทนที่สลิตคู่ได้นะครับ ไม่สามารถทำให้เฟสตรงกันได้ครับ)
เงื่อนไขของริ้วสว่าง ริ้วมืด
ผลต่างของระยะทางเชิงแสงของคลื่นแสงสองลูกซึ่งเดินทางมาแทรกสอดกันเรียกว่า ผลต่างเส้นทางแสง ครับ (Optical Path Difference: OPD)
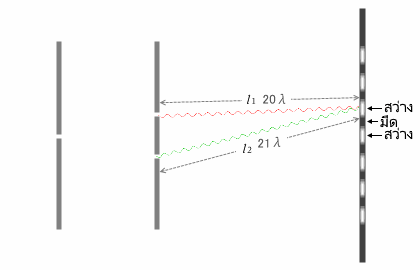สำหรับจุดที่มี OPD ของคลื่นแสงสองคลื่นที่เดินทางมาถึงฉากเป็นจำนวนเต็มเท่าของความยาวคลื่นจะเกิดการแทรกสอดแบบเสริมเป็นริ้วสว่างขึ้นครับ สำหรับจุดที่มี OPD เป็นจำนวนเต็มเท่าของความยาวคลื่นบวกกับอีกครึ่งหนึ่งของความยาวคลื่นจะเกิดเป็นริ้วมืดขึ้นครับ (อ้างอิงบทเงื่อนไขของการแทรกสอด ##link)
เงื่อนไขที่ทำให้เกิดริ้วสว่าง \(|l_1-l_2|=m\lambda\)
เงื่อนไขที่ทำให้เกิดริ้วมืด \(|l_1-l_2|=(m+{\large\frac{1}{2}})\lambda\)
\((m=0,1,2,...)\) ……\(①\)
ยกตัวอย่างเช่นในรูปด้านบน เมื่อคลื่นสีแดง มี \(l_1=20\lambda\), คลื่นสีเขียว มี \(l_2=21\lambda\) ได้ว่า \(|20\lambda-21\lambda|=1\lambda\) ซึ่งคือจุดที่ทำให้เกิดริ้วสว่างขึ้นครับ
ทีนี้ ลองมาคิดกันดูว่าสามารถเขียนค่า \(|l_1-l_2|\) นี้ให้อยู่ในรูปอื่นได้หรือไม่นะครับ
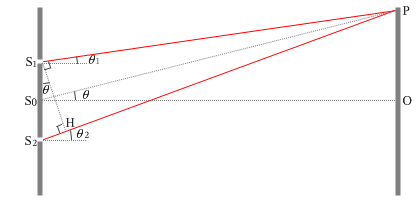เมื่อลองกำหนดสัญลักษณ์ตามรูปด้านซ้ายแล้ว จะสามารถมองว่าส่วนของเส้นตรงสามเส้น \(\rm{S_1 P,\;S_0 P,\;S_2 P}\) นั้นขนานกันได้ครับ เพราะว่าในความเป็นจริงแล้ว \(\rm{S_1 S_2}\) มีค่าน้อยกว่า \(\rm{1\;mm}\) และ \(\rm{S_0 O}\) มีค่ามากกว่า \(\rm{1\;m}\) ครับ ด้วยเหตุนี้ \(\rm{\angle S_2 S_1 H,\;\theta_1,\;\angle P S_0 O,\;\theta_2}\) จึงมีขนาดเท่ากันทั้งหมดครับ
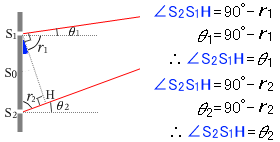สามารถมองออกไหมครับว่า\(\rm{\angle S_2 S_1 H}\) และ \(\theta_1\) มีขนาดเท่ากัน (\(\rm{\angle S_2 S_1 H}\) และ \(\theta_2\) ก็เท่ากันด้วย),
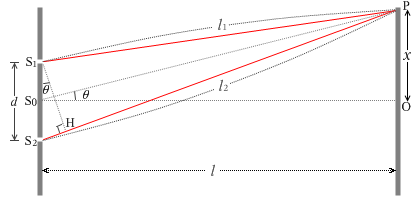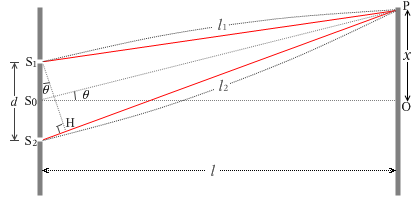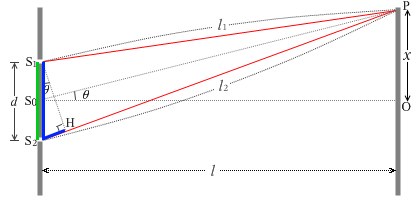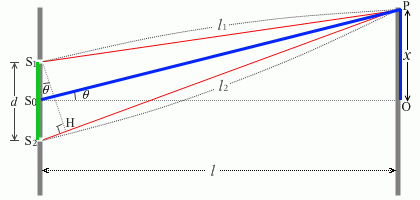นอกจากนี้เมื่อกำหนดสัญลักษณ์ตามรูปด้านซ้ายมือแล้ว (เกี่ยวกับเรื่องอัตราส่วนสามเหลี่ยม \(\sin\) ให้อ้างอิงบท \(\sin \cdot \cos\) link##
\(|l_1-l_2|\approx {\color{red}{\rm{S_2 H}}}={\color{lime}{\rm{S_1 S_2}} }{\color{blue}{\sin\theta}}={\color{lime}d}{\color{blue}{\sin\theta}}={\color{lime}d}{\color{blue}{\large\frac{x}{\rm{S_0 P}}}}\)
และเนื่องจาก \(\theta\) มีค่าน้อยมาก ๆ
\({\color{blue}{\large\frac{x}{\rm{S_0 P}}}}=\sin \theta\approx \tan \theta={\large\frac{x}{l}}\)
ดังนั้นจึงได้ว่า
\(|l_1-l_2|\approx {\large\frac{dx}{l}}\) ……\(②\)
ต่อไปจะอธิบายเกี่ยวกับ \(\sin \theta\approx \tan \theta\) นะครับ
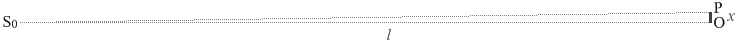
ในการทดลองการแทรกสอดโดยวิธีของยังนั้น ในความเป็นจริงแล้ว \(\triangle \rm{S_0 PO}\) จะมีลักษณะเป็นสามเหลี่ยมที่แบนมาก ๆ ตามรูปด้านบนครับ
ในกรณีนี้ที่ \(\theta\) มีค่าน้อยมาก ๆ และ \({\rm S_0 P}\approx l\) จะได้ว่า
\(\sin \theta={\large\frac{x}{S_0 P}}\approx {\large\frac{x}{l}}=\tan \theta\)
ครับ
(ในกรณีของการเลี้ยงเบนผ่านเกรตติ้งนั้นไม่มีความจำเป็นที่จะต้องทำการประมาณนี้ครับ เพราะว่า \(\theta\) มีค่ามากประมาณหนึ่ง ทำให้สามารถวัดมุมได้ครับ แต่ในกรณีที่ \(\theta\) มีขนาดเล็กมากจนไม่สามารถวัดค่าได้นั้น จำเป็นต้องทำการประมาณนี้ครับ )
ด้วยเหตุนี้ เมื่อแทนสมการที่ \(②\) เข้าไปในสมการที่ \(①\) จะได้ข้อสรุปตามด้านล่างนี้ครับ
การทดลองการแทรกสอดของแสงโดยวิธีของยัง
เงื่อนไขที่ทำให้เกิดริ้วสว่าง \(\boldsymbol{{\large\frac{dx}{l}}=m\lambda}\)
เงื่อนไขที่ทำให้เกิดริ้วมืด \(\boldsymbol{{\large\frac{dx}{l}}=(m+{\large\frac{1}{2}})\lambda}\)
\((m=0,1,2,...)\)
ระยะห่างระหว่างริ้วการแทรกสอด
จากสมการเงื่อนไขด้านบน จะลองทำการคำนวณหาระยะห่างระหว่างริ้วการแทรกสอดดูครับ เมื่อจัดรูปสมการเงื่อนไขของการเกิดริ้วสว่าง \({\large\frac{dx}{l}}=m\lambda\) จะได้ \(x={\large\frac{ml\lambda}{d}}\) ในที่นี้ ตัวแปร \(m\) นี้จะบ่งบอกว่า ริ้วนั้น ๆ อยู่ห่างจากแนวกึ่งกลางเป็นลำดับที่เท่าไหร่ครับ
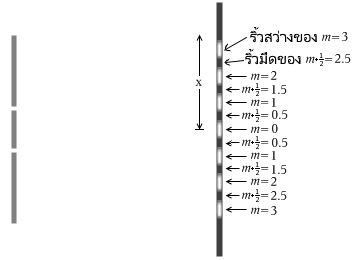เมื่อ OPD ของคลื่นแสงสองคลื่นเท่ากับ \(0\) จะนับเป็นลำดับที่ \(0\) พูดอีกอย่างคือแนวกึ่งกลางครับ
ในภาพด้านบนนั้น ได้ทำการยกตัวอย่างกรณีที่ คลื่นสีแดง \(l_1=20\lambda\), คลื่นสีเขียว มี \(l_2=21\lambda\) ได้ว่า \(|20\lambda-21\lambda|=1\lambda\) นี่คือกรณีที่ \(m=1\) ครับ
เมื่อ OPD มีขนาดมากขึ้น \(m\) (และ \(x\) ด้วย) ก็จะมีขนาดมากขึ้นตามครับ
และด้วยหลักการนี้แล้ว ระยะห่างระหว่างริ้ว \({\mathit{\Delta}} x\) จะเท่ากับ \(x_{m+1} - x_m\) ครับ
\begin{align} \hspace{30pt}{\mathit{\Delta}} x&=x_{m+1} - x_m \\\\ &={\frac{(m+1)l\lambda}{d}}-{\frac{ml\lambda}{d}} \\\\ &={\frac{l\lambda}{d}} \end{align}
เมื่อใช้สมการนี้แล้ว ก็จะสามารถหาค่าความยาวคลื่น \(\lambda\) ของคลื่นแสงได้จาก ระยะห่างระหว่างริ้ว \({\mathit{\Delta}} x\), ระยะจนถึงฉาก \(l\) และระยะห่างระหว่างสลิต \(d\) ครับ หรือทำความเข้าใจในอีกมุมหนึ่งได้ว่า ระยะห่างระหว่างริ้ว \({\mathit{\Delta}} x\) จะมากขึ้นได้เมื่อ \(l\) หรือ \(\lambda\) มีค่ามากขึ้น หรือค่า \(d\) มีขนาดเล็กลง
เพิ่มเติมนะครับ การทำให้ \(d\) (ระยะห่างระหว่างสลิต) มีค่าน้อยลงนั้น จะมีลักษณะเหมือนกับในรูปประกอบด้านล่างครับ
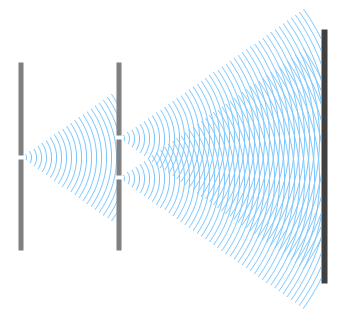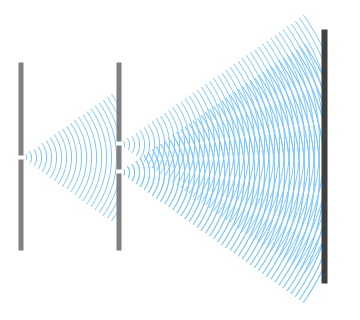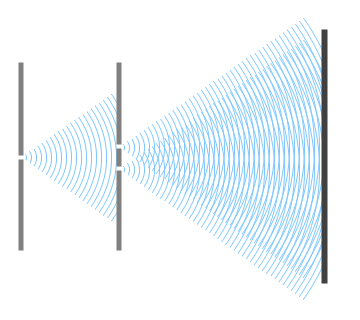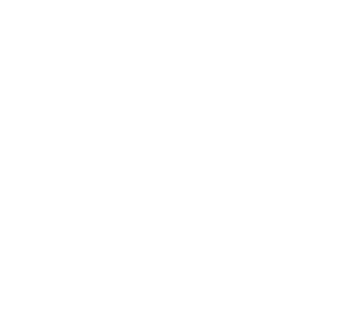ผมคิดว่าน่าจะมองเห็นว่าระยะห่างระหว่างริ้วจะกว้างขึ้นนะครับ เป็นหลักการเดียวกับการเกิดลายมัวเร (Moire Pattern) ##link ครับ
วิธีทำอื่น ๆ
ต่อไปจะทำการแสดงอีกวิธีการในการทำให้ได้สมการที่ \(②\) \(|l_1-l_2|\approx {\large\frac{dx}{l}}\) มานะครับ
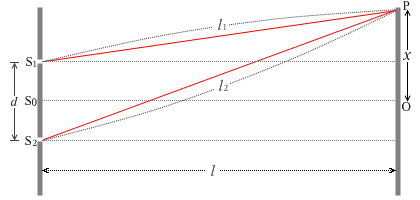
จากทฤษฏีบทพีทาโกรัส
\(\hspace{30pt} l_{1}^{2}=l^{2}+\left(x-\frac{d}{2}\right)^{2}\)
นั่นคือ
\begin{align} \hspace{30pt} l &=\sqrt{l^{2}+\left(x-\frac{d}{2}\right)^{2}} & &=\sqrt{l^{2}\left\{1+\left(\frac{x-\frac{d}{2}}{l}\right)^{2}\right\}} \\ &=l \sqrt{1+\left(\frac{x-\frac{d}{2}}{l}\right)^{2}} & &=l\left\{1+\left(\frac{x-\frac{d}{2}}{l}\right)^{2}\right\}^{\frac{1}{2}} \end{align}
ในสมการนี้ หากว่า \(x\) และ \(d\) มีค่าน้อยกว่า \(l\) เพียงพอ สามารถประยุกต์ใช้สูตรการประมาณ \((1+a)^n\approx 1+na\) นี้ได้ครับ (เมื่อ \(a\) มีค่าน้อยมาก ๆ) ผมจะไม่ทำการอธิบายวิธีการได้มาของสูตรการประมาณนี้ ณ ที่นี้นะครับ แต่สำหรับคนที่สนใจ ลองสืบค้นโดยใช้ keyword 「อนุกรมเทย์เลอร์ การประมาณ」หรือ「Taylor Series Approximation」ดูนะครับ
เมื่อทำการประมาณ จะได้ว่า
\(\hspace{30pt}l_{1} \approx l\left\{1+\frac{1}{2}\left(\frac{x-\frac{d}{2}}{l}\right)^{2}\right\}\)
ด้วยหลักการเดียวกันหาค่า \(l_2\) จะได้ว่า
\(\hspace{30pt}l_{2} \approx l\left\{1+\frac{1}{2}\left(\frac{x+\frac{d}{2}}{l}\right)^{2}\right\}\)
ดังนั้นจะสามารถหา Path Difference ได้เท่ากับ
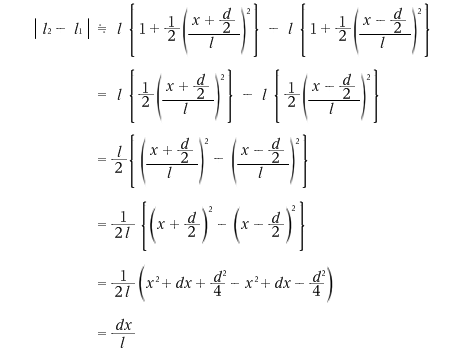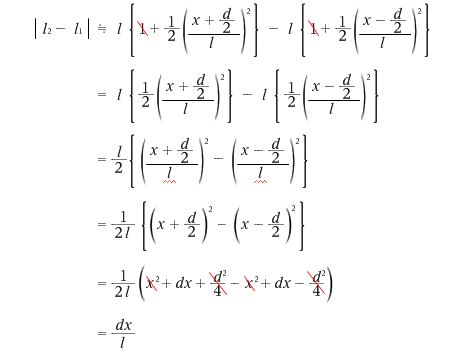
ครับ
ความคิดเห็น
แสดงความคิดเห็น