กระจกเว้า

ภาพที่กระจกเว้าสร้าง

หาความสัมพันธ์ระหว่างทุกปริมาณ

จะลองคิดถึงความสัมพันธ์ของตัวแปรเหล่านี้ เวลาที่รังสีแสงที่ออกจากวัตถุ สะท้อนที่กระจกเว้า และเกิดเป็นภาพขึ้นดูครับ

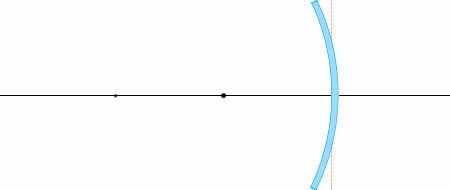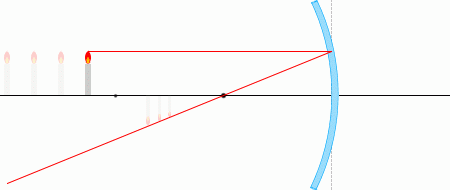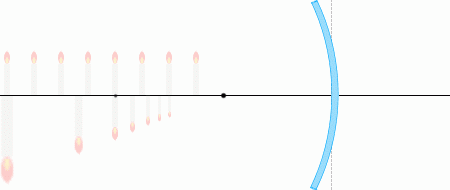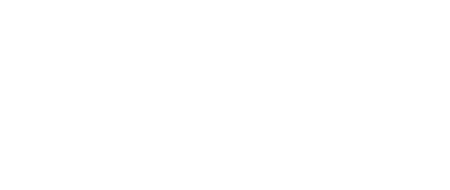
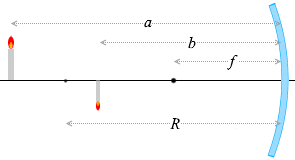ระยะจากวัตถุถึงกระจก \(:a\)
ระยะจากกระจกถึงภาพ \(:b\)
ระยะโฟกัส \(:f\)
รัศมีทรงกลม \(:R\)

รังสีแสงที่ใช้เป็นตัวแทน

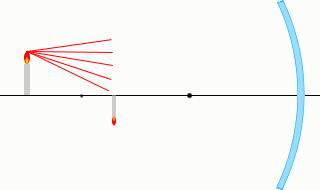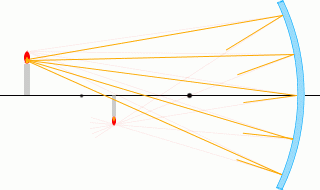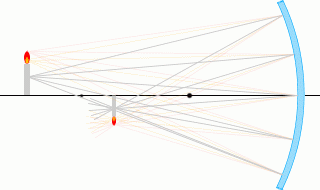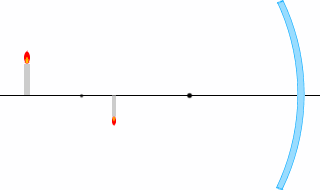เพื่อจะตอบคำถามที่ว่า "จะเกิดภาพแบบไหนขึ้น" แน่นอนว่าถ้าเราคิดถึงการเดินทางของรังสีแสงทุกเส้น ก็จะได้คำตอบครับ

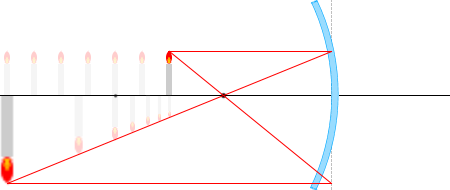
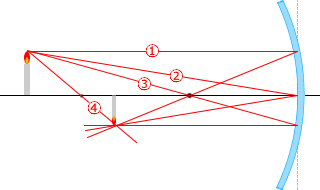แต่ ถ้าหากว่าเราคำนวณแค่รังสีแสงที่ออกมาจากปลายยอดของวัตถุตามรูปด้านซ้ายแล้ว ก็เพียงพอที่จะสามารถระบุได้ว่า ภาพเกิดที่ตำแหน่งใด และมีขนาดเท่าใดครับ

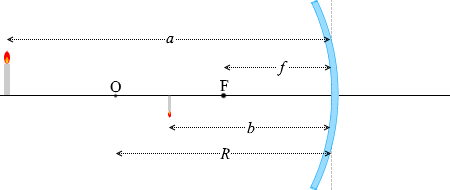
\(\hspace{6pt}\color{red}{①}\) รังสีแสงที่ขนานกับแกนแสงจะสะท้อนกลับและเดินทางผ่านจุดโฟกัส
\(\hspace{6pt}\color{red}{②}\) จากกฏการสะท้อน มุมตกกระทบ = มุมสะท้อน
\(\hspace{6pt}\color{red}{③}\) รังสีแสงที่ผ่านจุดโฟกัสจะสะท้อนกลับและเดินทางขนานไปกับ แกนแสง
\(\hspace{6pt}\color{red}{④}\) รังสีแสงที่ผ่านจุดศูนย์กลางทรงกลมจะสะท้อนกลับและและผ่านจุดศูนย์กลางอีกรอบ

จากนี้ จะใช้รังสีแสง 2 เส้นใด ๆ จากในบรรดา 4 เส้นนี้ในการคิดต่อไปครับ มีวิธีคิดมากมายครับ

ทรงกลมที่มีความโค้งน้อย

ผมได้อธิบายไปเล็กน้อยแล้วในบท 『กระจกเงาทรงกลม』 ครับว่า การจะผูกรวมรังสีแสงเข้าด้วยกันไว้ที่จุดโฟกัสนั้น จะใช้เพียงส่วนเล็ก ๆ ของทรงกลมครับ ＊ ปิด จะใช้ทรงกลมที่มีรัศมีใหญ่ครับ เป็นทรงกลมที่โค้งหลวม ๆ ช้า ๆ ครับ เป็นทรงกลมที่มีความโค้งน้อยครับ

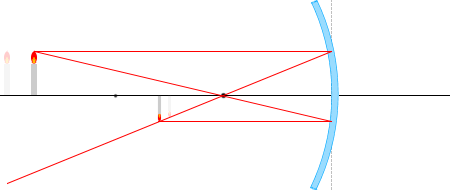
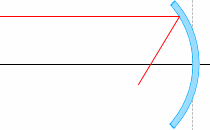สำหรับบทนี้ แม้ว่าความจริงแล้วแสงควรจะสะท้อนแบบนี้ แต่ผมจะละเลยส่วนโค้งนี้ไป และ

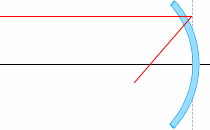วาดอธิบายแบบนี้แทนนะครับ อยากให้ระลึกไว้ด้วยนะครับ

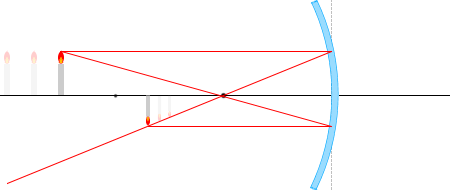
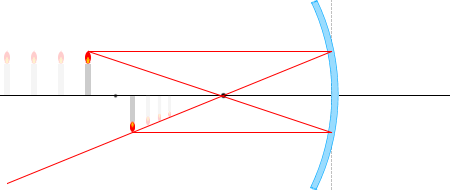
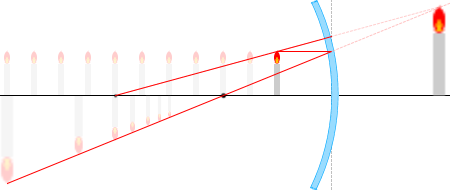
เวลาที่วางวัตถุไว้ไกลกว่าจุดโฟกัส

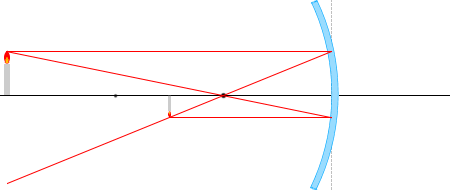
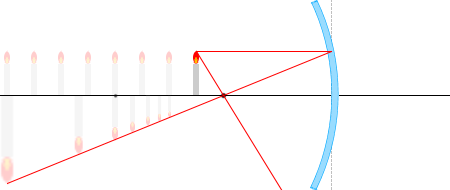
ในบรรดารังสีแสงที่เขียนไว้ด้านบนนั้น จะลองเอารังสี \(\color{red}{①}\) และ\(\color{red}{③}\) และสามเหลี่ยมที่เกิดจากรังสีทั้งสองนี้ มาพิจารณาดูครับ

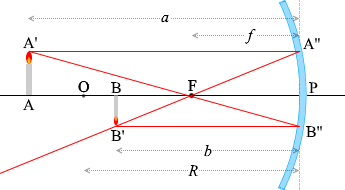กำหนดตัวแปรตามรูปซ้ายมือครับ

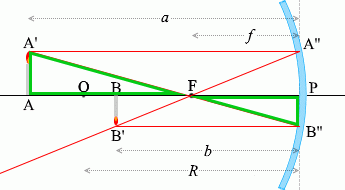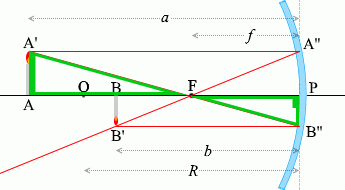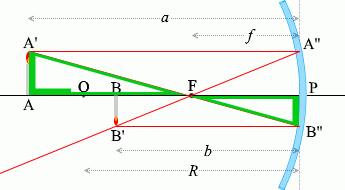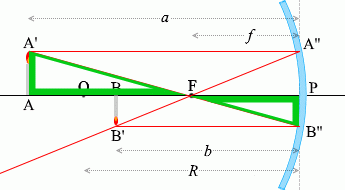เนื่องจาก (สามารถมองว่า) \(\color{green}{\triangle {\rm AA'F}}\) คล้ายกับ \(\color{green}{\triangle {\rm PB''F}}\) ได้ ดังนั้น

　　\({\rm\large{\frac{P B^{\prime \prime}}{A A^{\prime}}}=\large{\frac{P F}{A F}}}=\large{\frac{f}{a-f}}\)

และนอกจากนี้ เนื่องจาก PB" = BB' เมื่อแทนลงในสมการด้านบนจะได้

　　\({\rm\large{\frac{B B'}{A A'}}}=\large{\frac{f}{a-f}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ①\)

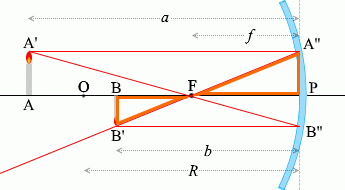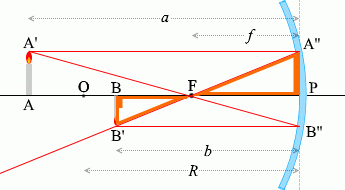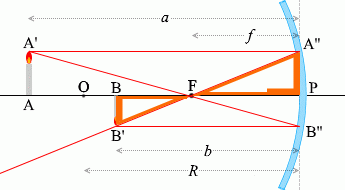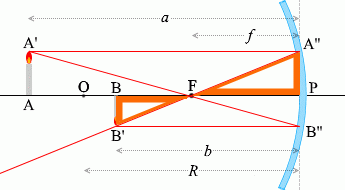เนื่องจาก \(\color{orange}{\triangle {\rm PA''F}}\) คล้ายกับ \(\color{orange}{\triangle {\rm BB'F}}\) ดังนั้น

　　\({\rm\large{\frac{B B'}{P A''}}=\large{\frac{B F}{P F}}}=\large{\frac{b-f}{f}}\)

และนอกจากนี้ เนื่องจาก PA" = AA' เมื่อแทนลงในสมการด้านบนจะได้

　　\({\rm\large{\frac{B B'}{A A'}}}=\large{\frac{b-f}{f}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ②\)

เนื่องจากสมการ \(①\) และสมการ \(②\) มีด้านซ้ายมือร่วมกัน ดังนั้น

\(\hspace{18pt}\large{\frac{f}{a-f}}=\large{\frac{b-f}{f}}\)

\(\therefore \hspace{12pt} f^{2}=(b-f)(a-f) \)

\(\therefore \hspace{12pt} f^{2}=a b-b f-a f+f^{2} \)

\(\therefore \hspace{12pt} 0=a b-b f-a f+0 \)

\(\therefore \hspace{12pt} bf + af = ab \hspace{18pt}\) หารด้วย \(abf\) ทั้งสองข้าง

\(\therefore \hspace{12pt} \large{\frac{b f}{a b f}}+\large{\frac{a f}{a b f}}=\large{\frac{a b}{a b f}} \)

\(\therefore \hspace{12pt} \large{\frac{1}{a}}+\large{\frac{1}{b}}=\large{\frac{1}{f}} \hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ③\)

เรียกสมการนี้ว่าสูตรการเกิดภาพครับ เหมือนกับสูตรกาารเกิดภาพสำหรับเลนส์ครับ เราสามารถใช้สูตรเดียวกันนี้อธิบายได้ครับ หากว่าเรากำหนดเครื่องหมายบวกลบของตัวแปร \(a,b,f\) อย่างเหมาะสม

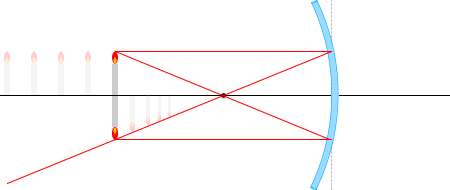
ถ้าลองดูสมการนี้ดี ๆ จะเห็นว่า เมื่อ \(a → ∞\) (พจน์แรกของฝั่งซ้ายมือเป็น \(0\)) แล้ว \(b=f\) ครับ สอดคล้องกับนิยามของพาราโบลาครับ นอกจากนี้ ดังที่จะอธิบายต่อไปจากนี้ เนื่องจากกำลังขยายเท่ากับ \(\large{\frac{b}{a}}\) ในกรณีที่ \(a → ∞\) ก็จะประมาณ \(0\) ครับ ถ้าหากวางวัตถุไว้ไกลจากกระจกเว้ามาก ๆ จะเกิดภาพขนาดเล็กมาก ๆ ใกล้ ๆ กับจุดโฟกัสนั่นเองครับ

กำลังขยาย

จะลองคิดเกี่ยวกับกำลังขยายดู แบบเดียวกับในกรณีของเลนส์นะครับ กำหนดแทนด้วย \(m\) ไว้ก่อนครับ ＊ มาจาก magnification (กำลังขยาย) ปิด

กำลังขยาย คือ อัตราส่วนที่บอกว่าวัตถุถูกขยายขึ้นเท่าไหร่ หดเล็กลงเท่าไหร่ พูดอีกอย่างก็คือ \({\rm\large{\frac{B B'}{A A'}}}\) ครับ และจากสมการ \(①\)

\(m={\rm\large{\frac{B B'}{A A'}}}=\large{\frac{f}{a-f}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ④\)

ครับ นอกจากนี้ จากสมการ \(③\)

\(\hspace{10pt}\large{\frac{1}{a}}+\large{\frac{1}{b}}=\large{\frac{1}{f}}\)

\(\therefore\hspace{12pt}\large{\frac{b+a}{ab}}=\large{\frac{1}{f}}\)

\(\therefore\hspace{12pt}\large{\frac{ab}{a+b}}=f\)

ถ้าเอาสิ่งนี้ไปแทนในสมการ \(④\) แล้วจะกลายเป็นแบบนี้

\(m=\large{\frac{\frac{a b}{a+b}}{a-\frac{a b}{a+b}}}=\large{\frac{a b}{\left(a^{2}+a b\right)-a b}}=\large{\frac{a b}{a^{2}}}=\large{\frac{b}{a}}\)

ครับ

แม้ว่าจะอธิบายแบบนี้มาก็ตามแต่หากว่า

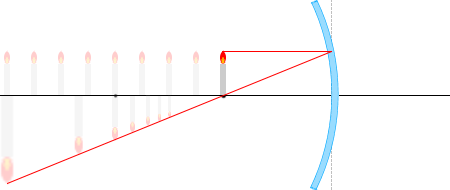
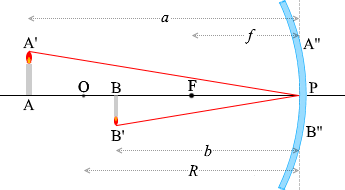ลองพิจารณาดู \({\triangle {\rm AA'P}}\) และ \({\triangle {\rm BB'P}}\) ที่เกิดจากรังสี \(\color{red}{②}\) ซึ่งเป็นหนึ่งในรังสีแสงที่ใช้เป็นตัวแทนดังที่ได้อธิบายไว้ ด้านบน ก็จะเห็นได้ชัดเลยว่า \(m=\large{\frac{b}{a}}\) ครับ

กำลังขยายของภาพ ก็คือ อัตราส่วนของระยะ(จากวัตถุและจากภาพ) จนถึงกระจกนั่นเองครับ

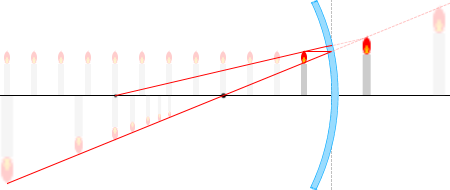
ระหว่าง O และ F

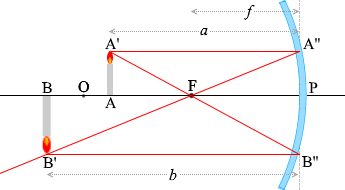ในกรณีที่วางวัตถุ AA' ไว้ระหว่างจุดศูนย์กลางทรงกลม O และจุดโฟกัส F นั้น เราก็สามารถหา สมการความสัมพันธ์ (สูตรการเกิดภาพ) เดียวกันนี้ออกมาได้ครับ เพื่อทำให้แน่ใจ จะลองตรวจสอบดูครับ

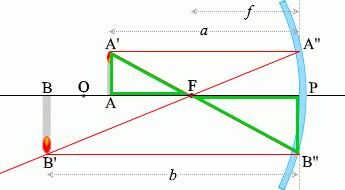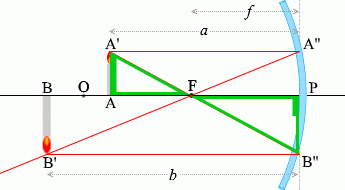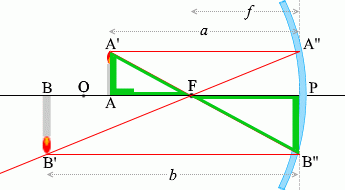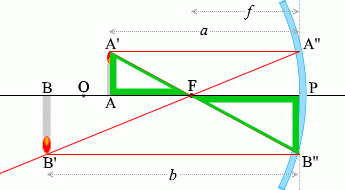เนื่องจาก \(\color{green}{\triangle {\rm AA'F}}\) คล้ายกับ \(\color{green}{\triangle {\rm PB''F}}\) ดังนั้น

　　\({\rm\large{\frac{P B^{\prime \prime}}{A A^{\prime}}}=\large{\frac{P F}{A F}}}=\large{\frac{f}{a-f}}\)

และนอกจากนี้ เนื่องจาก PB" = BB' เมื่อแทนลงในสมการด้านบนจะได้

　　\({\rm\large{\frac{B B'}{A A'}}}=\large{\frac{f}{a-f}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot\) เหมือนกับสมการ \(①\) ด้านบน

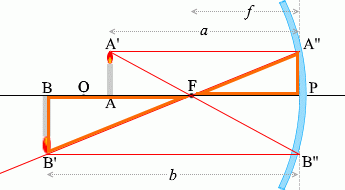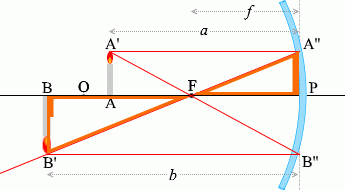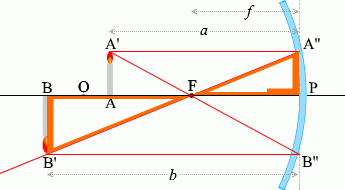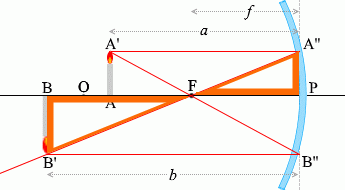เนื่องจาก \(\color{orange}{\triangle {\rm PA''F}}\) คล้ายกับ \(\color{orange}{\triangle {\rm BB'F}}\) ดังนั้น

　　\({\rm\large{\frac{B B'}{P A''}}=\large{\frac{B F}{P F}}}=\large{\frac{b-f}{f}}\)

และนอกจากนี้ เนื่องจาก PA" = AA' เมื่อแทนลงในสมการด้านบนจะได้

　　\({\rm\large{\frac{B B'}{A A'}}}=\large{\frac{b-f}{f}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot\) เหมือนกับสมการ \(②\) ด้านบน

ถ้านำสูตรเหล่านี้ไปคำนวณต่อ ก็จะได้ผลลัพธ์แบบเดียวกับด้านบนครับ

ภาพหัวกลับ

จนถึงตอนนี้ ภาพที่อธิบายมาเป็นภาพ หัวกลับ ทุกภาพ หากว่านำฉากไปวางไว้ที่ตำแหน่ง BB' ก็จะปรากฏภาพออกมา จึงเป็น ภาพจริงครับ ในทางกลับกัน ภาพของหัวข้อ 『เวลาที่วางวัตถุไว้ใกล้กว่าจุดโฟกัส』ซึ่งจะอธิบายต่อไปนี้นั้น เป็นภาพเสมือนครับ เป็นภาพที่มนุษย์ 'เห็น' ได้ในสมองเท่านั้นครับ

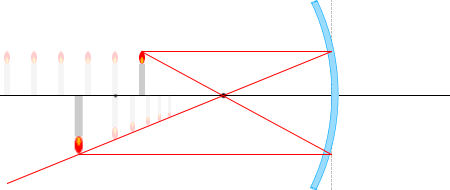
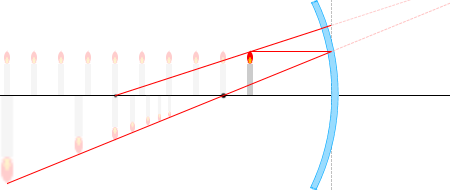
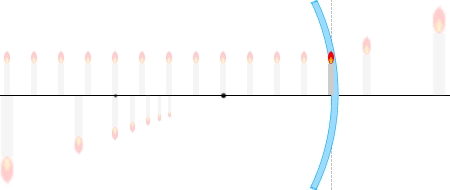
เวลาที่วางวัตถุไว้ใกล้กว่าจุดโฟกัส

เวลาที่วางวัตถุไว้ใกล้กว่าจุดโฟกัส \(b\) จะมีค่าเป็นลบครับ เกิดภาพขึ้นที่ฝั่งตรงข้ามของกระจกครับ (ด้านหลัง)

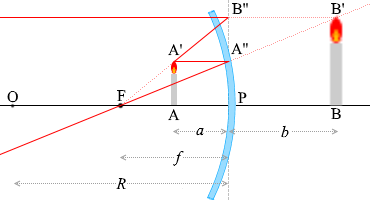ในบรรดารังสีแสงที่เขียนไว้ด้านบนนั้น จะลองเอารังสี \(\color{red}{③}\) และ\(\color{red}{①}\) และสามเหลี่ยมที่เกิดจากรังสีทั้งสองนี้ มาพิจารณาดูครับ

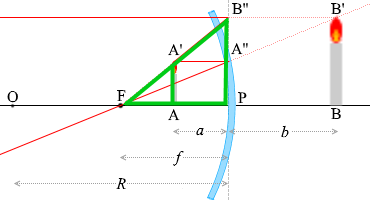เนื่องจาก \(\color{green}{\triangle {\rm AA'F}}\) คล้ายกับ \(\color{green}{\triangle {\rm PB''F}}\) ดังนั้น

　　\({\rm\large{\frac{P B^{\prime \prime}}{A A^{\prime}}}=\large{\frac{P F}{A F}}}=\large{\frac{f}{f-a}}\)

และนอกจากนี้ เนื่องจาก PB" = BB' เมื่อแทนลงในสมการด้านบนจะได้

　　\({\rm\large{\frac{B B'}{A A'}}}=\large{\frac{f}{f-a}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ①'\)

เนื่องจาก \(\color{orange}{\triangle {\rm PA''F}}\) คล้ายกับ \(\color{orange}{\triangle {\rm BB'F}}\) ดังนั้น

　　\({\rm\large{\frac{B B'}{P A''}}=\large{\frac{B F}{P F}}}=\large{\frac{b+f}{f}}\)

และนอกจากนี้ เนื่องจาก PA" = AA' เมื่อแทนลงในสมการด้านบนจะได้

　　\({\rm\large{\frac{B B'}{A A'}}}=\large{\frac{b+f}{f}}\hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ②'\)

เนื่องจากสมการ \(①'\) และสมการ \(②'\) มีด้านซ้ายมือร่วมกัน ดังนั้น

\(\hspace{18pt}\large{\frac{f}{f-a}}=\large{\frac{b+f}{f}}\)

\(\therefore \hspace{12pt} f^{2}=(b+f)(f-a) \)

\(\therefore \hspace{12pt} f^{2}=b f+f^{2}-a b-a f \)

\(\therefore \hspace{12pt} 0=bf + 0 - ab -af \)

\(\therefore \hspace{12pt} ab = bf-af \)

\(\therefore \hspace{12pt} bf - af = ab \hspace{18pt}\) หารด้วย \(abf\) ทั้งสองข้าง

\(\therefore \hspace{12pt} \large{\frac{b f}{a b f}}-\large{\frac{a f}{a b f}}=\large{\frac{a b}{a b f}}\hspace{12pt} \)

\(\therefore \hspace{12pt} \large{\frac{1}{a}}-\large{\frac{1}{b}}=\large{\frac{1}{f}} \hspace{12pt} \cdot\cdot\cdot\cdot\cdot\cdot ③'\)

สมการนี้สามารถมองว่าเป็นแบบนี้ได้ครับ
\(\large{\frac{1}{a}}+\large{\frac{1}{(-b)}}=\large{\frac{1}{f}}\)

กำลังขยาย

สำหรับกำลังขยายในกรณีนี้

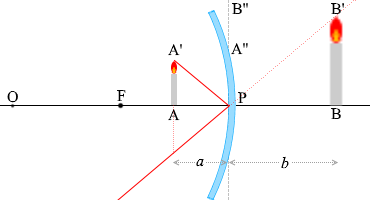เมื่อพิจารณาที่สามเหลี่ยมที่เกิดจากรังสีแสงที่เป็นตัวแทน \(\color{red}{②}\) ตามที่ได้แสดงไว้ด้านบนแล้วจะเห็นว่า

　　\(m=\large{\frac{b}{a}}\)

ครับ

ภาพเสมือนหัวตั้ง

เวลาที่มองภาพที่ได้ครั้งนี้จากด้านหน้ากระจก (สำหรับรูปด้านซ้ายคือด้านซ้ายมือของกระจก) มนุษย์จะรู้สึกในสมองราวกับว่าภาพนั้นอยู่ที่ด้านหลัง (ด้านตรงข้าม) กระจกครับ พูดอีกอย่างก็คือภาพเสมือนครับ และยังไม่ใช่ภาพหัวกลับแต่เป็นภาพหัวตั้งครับ

ระยะโฟกัสคือครึ่งหนึ่งของรัศมี

ต่อไป จะค้นหาความสัมพันธ์ระหว่างระยะโฟกัสและและรัศมีดูครับ

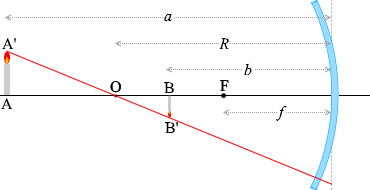เมื่อพิจารณาดูสามเหลี่ยมที่เกิดจากรังสีแสง \(\color{red}{④}\) ที่เป็นรังสีตัวแทน ตามที่ได้แสดงไว้ด้านบนแล้วจะเห็นว่า เนื่องจาก \(\triangle {\rm AA’O}\) คล้ายกับ \(\triangle {\rm BB’O}\) ดังนั้น

　　\({\rm\large{\frac{B B^{\prime}}{A A^{\prime}}}=\large{\frac{BO}{A O}}}=\large{\frac{R-b}{a-R}}\)

เมื่อรวมเข้ากับสูตรกำลังขยายที่อธิบายไว้ด้านบน

　　\(m={\rm\large{\frac{B B^{\prime}}{A A^{\prime}}}}=\large{\frac{b}{a}}\)

จะได้ว่า

\(\hspace{18pt}\large{\frac{R-b}{a-R}}=\large{\frac{b}{a}}\)

\(\therefore \hspace{12pt} a R-a b=a b-b R \)

\(\therefore \hspace{12pt} a R+b R=2 a b \hspace{18pt}\) หารด้วย \(abR\) ทั้งสองข้าง

\(\therefore \hspace{12pt} \large{\frac{a R}{a b R}}+\large{\frac{b R}{a b R}}=\large{\frac{2ab}{a b R}}\)

\(\therefore \hspace{12pt} \large{\frac{1}{b}}+\large{\frac{1}{a}}=\large{\frac{2}{R}}\)

\(\therefore \hspace{12pt} \large{\frac{1}{a}}+\large{\frac{1}{b}}=\large{\frac{2}{R}}\)

เมื่อลองเปรียบเทียบสูตรนี้เข้ากับสูตรการเกิดภาพ \(③\)

\(\large{\frac{1}{a}}+\large{\frac{1}{b}}=\large{\frac{1}{f}}\)

ได้ว่า

\(\hspace{18pt}\large{\frac{1}{f}}=\large{\frac{2}{R}}\)

\(\therefore \hspace{12pt} f=\large{\frac{R}{2}}\)

นั่นคือระยะโฟกัสคือครึ่งหนึ่งของรัศมีครับ ＊ คำอธิบายผู้แปล : ถึงตรงนี้อาจจะงงกับการจัดสมการที่ยาวเหยียด และ เกิดคำถามว่าจะรู้ได้ยังไงว่าต้องคิดแบบนี้ ? ต้องมาทางนี้ ? มันไม่บังเอิญไปหน่อยหรอที่จัดไปจัดมาแล้วได้แบบนี้ ? บังเอิญครับ แต่ว่ามีหลักการพอจะช่วยคลำทางได้ อย่าเพิ่งเสียกำลังใจไปครับ! หลักการอยู่ที่ว่าเราพยายามหาความสัมพันธ์ \(a,b,R\) และจัดให้ได้พจน์ทางซ้ายมือ \(\large{\frac{1}{a}}+\large{\frac{1}{b}}\) เพื่อจะเปรียบเทียบกับสมการ \(③\) ครับ จากมุมมองคนอ่าน สมการความสัมพันธ์ \(f=\large{\frac{R}{2}}\) อาจจะดูเหมือนเป็นสูตรตายตัวที่ต้องท่องจำ แต่ว่าอยากให้ลองจินตนาการนึกถึงภาพของนักคณิตศาสตร์คนแรก ๆ ที่หาสูตรนี้ออกมา ที่อยู่ในยุคที่สูตรนี้ยังไม่อยู่ในหนังสือเรียน และไม่รู้ด้วยซ้ำว่ามีความสัมพันธ์นี้อยู่ เขาก็ต้องคลำอยู่ในความมืดแบบเดียวกับเรานี่แหละครับ เพราะฉะนั้นสำหรับคำถามที่ว่า "จะรู้ได้อย่างไรว่าต้องมาทางนี้ คิดแบบนี้" คงพอจะได้คำตอบแล้วสินะครับ ปิด

สรุปของกระจกเว้า

จะลองรวมสูตรการเกิดภาพสำหรับกรณีที่วางวัตถุไว้ไกลกว่าและใกล้กว่าจุดโฟกัสเข้าเป็นหนึ่งเดียวดูนะครับ นั่นคือจะรวมสมการ \(③\) และสมการ \(③'\) เข้าด้วยกันครับ กำหนดให้ \(b\) สามารถมีค่าเป็นลบได้ด้วยครับโดยให้เวลาที่เกิดภาพด้านหลังกระจกแทน \(b\) ด้วยลบครับ ลองดู『สรุปของกระจกเงาทรงกลม』 อ้างอิงด้วยนะครับ

\(\large{\frac{1}{a}}+\large{\frac{1}{b}}=\large{\frac{1}{f}}\)

เวลาที่ \(a \gt f\) : \(b \gt 0\) และ เกิดภาพจริงหัวกลับ
เวลาที่ \(a \lt f\) : \(b \lt 0\) และ เกิดภาพเสมือนหัวตั้ง

\(m=\large{\frac{|b|}{a}}\)